株式投資をするに当たっては、投じる資金と同程度(あるいはそれ以上に)利回りを考えることが大切です。
利回りがいかに重要かを、簡単なシミュレーションで考えてみます。
利回りとは、配当(あるいは利息)÷株価で計算されます。例えば、100万円に対して1年後に1万円の配当が得られるならば、利回りは1÷100=0.01=1%です。
ここでは、単純化のため、株式や債券のように資産そのものの変動はないものとして考えます。
1. 複利を考える
年間にいくらかのお金を積み立てていく場合、銀行であれば1年後に決まった額のお金(利息)を得ることができます。例えば100万円を口座に入れておき、年利が1%ならば、1年後に1万円の利息がつきます。100万円+(100万円×0.01)=100万円×(1+0.01)=101万円。
ここで、2年目にあたり、先ほどの1万円を引き出すこともできますが、そのままにしておきます。さらに100万円追加するとします。
資産額=100万円×(1+0.01)+100万円=201万円
こうして1年経過した場合、3年目の初めには口座に以下の資産があることにになります。
資産額=(100万円×(1+0.01)+100万円)×(1+0.01)=201万円×1.01=203.01万円
これを繰り返していくと、いくらになるでしょうか。
上記のケースで10年投資した場合は表のような結果になります。

最終的に、資産合計は投入した金額1000万円+利息分46万円=1046万円となります。複利の資産増加の効果はこのように計算できます。
2. 利回りの違いによる複利の効果の違い
ここでは、利回りの違いが資産増加に与える影響の違いを検討します。以下の3ケースを想定します。前節のシミュレーションと同じく、受け取り利息は全て再投資することとします。
- ケース1 利回り1%、1年の投入金額100万円
- ケース2 利回り1%、1年の投入金額110万円
- ケース3 利回り5%、1年の投入金額100万円
さて、10年後の総資産はいずれのケースが一番多くなっているでしょうか。
結果は次のようになります。
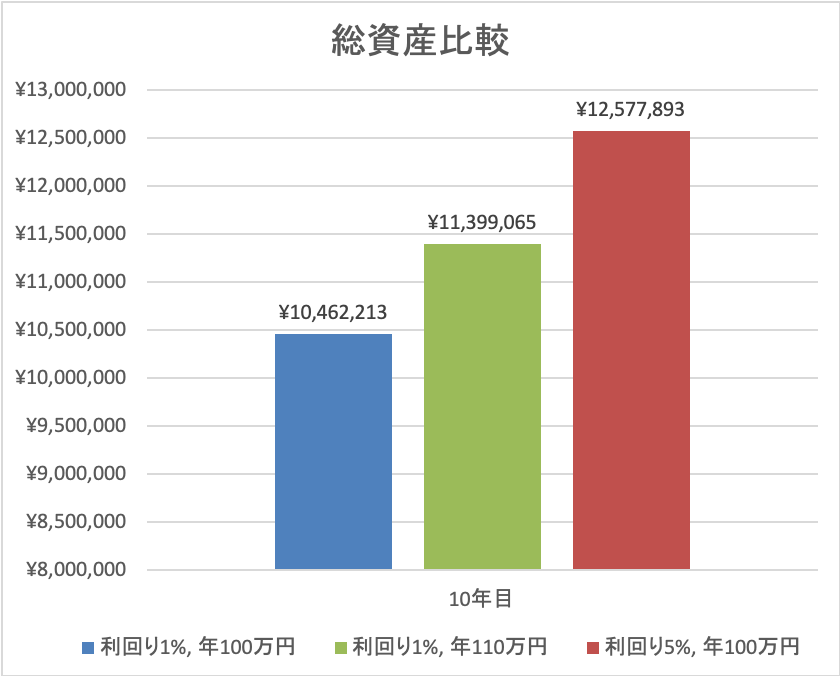
最終的には、ケース3の利回り5%、年100万円の結果が、ケース1の利回り1%、年100万円を200万円程度上回ります。ケース2の利回り1%、年110万円の結果をも凌いでいるのは、直感的には把握しにくく、意外に思われるのではないでしょうか。
これは、次の図のように利息の違いを比較してみると理解できます。
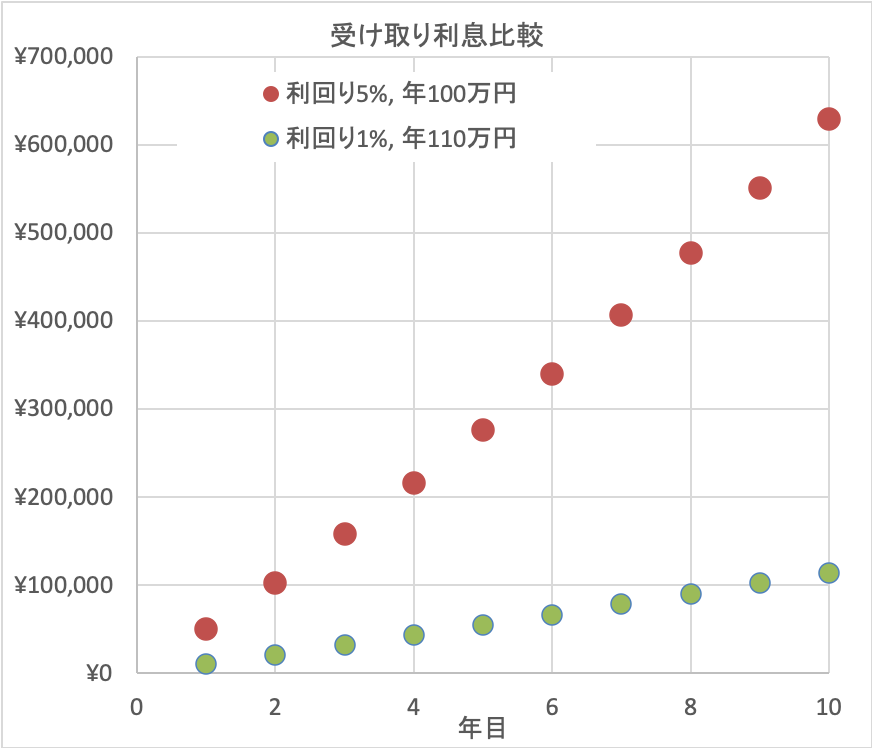
ケース3の利回り5%、100万円投入の条件が、受け取り利息が多くなり、資産増加に大きな影響を与えていることがわかります。
繰り返しますが、株式投資をするに当たっては、投じる資金と同程度(あるいはそれ以上に)利回りを考えることが大切です。

