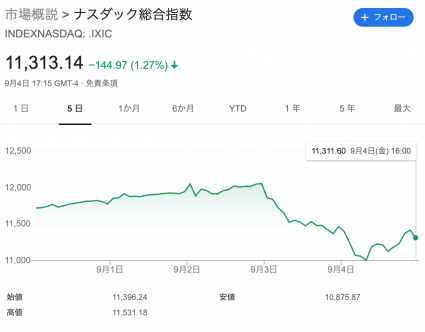
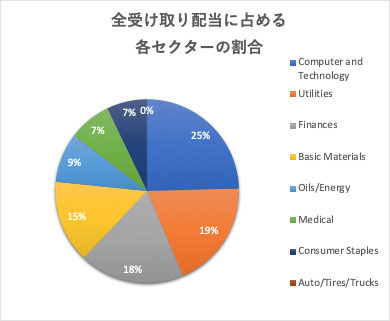
前回の投稿では、効率的市場仮説、ランダムウォーク、ブラウン運動という考え方に立つなら、過去の株価データから未来の株価は予測できないということを説明しました。
今回は、上記の考え方を否定する根拠について見ていきます。
- 市場のファットテール
- 株価の過去に対する依存性
1.ファットテール
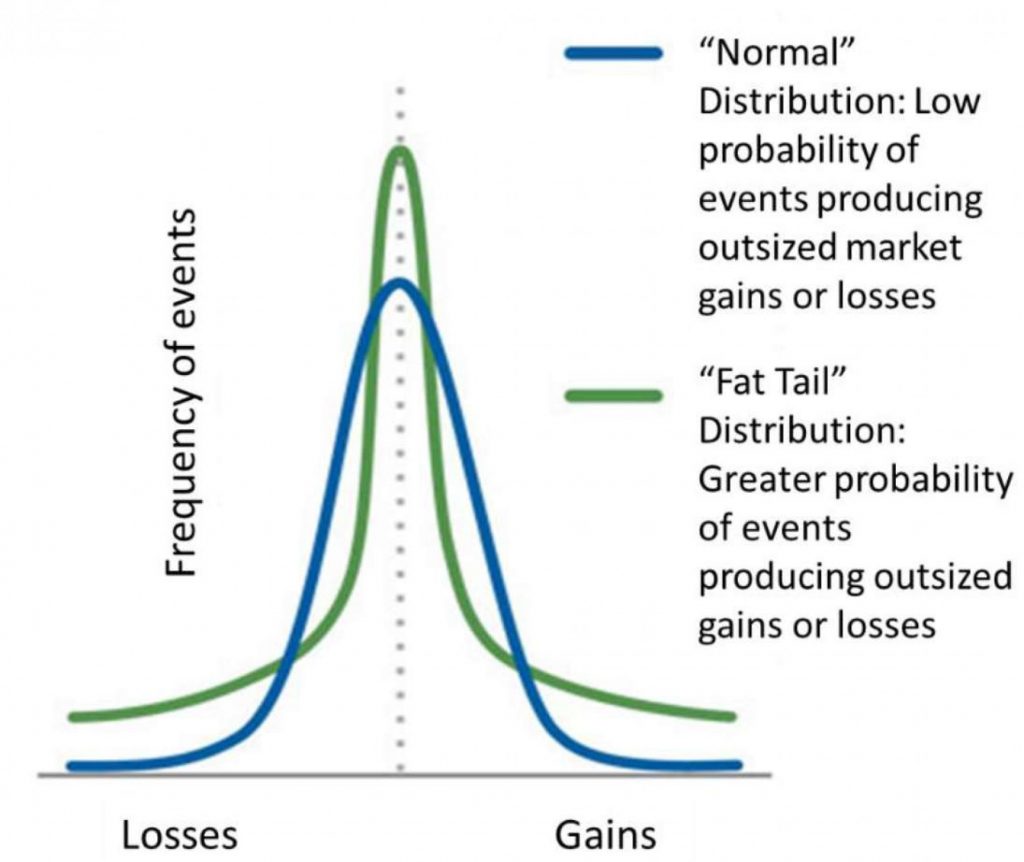
株価の対数収益率は正規分布になるのが、ブラウン運動の条件でした。実際は、冒頭図のようなファットテールと呼ばれる分布(図1)になります。
ファットテールだと正規分布とは次の点で違います。
正規分布よりも、リスク(ここではボラティリティ、価格変動)が増える。
つまり、正規分布を前提としたモデルでは、分布の端にある極端な変動の発生確率を過少評価してしまうのです。
リーマンショックでは、正規分布(またはその修正)モデルを前提として商品開発をしていたので、大暴落(ブラックスワン)を過小評価して、大惨事になりました。有名なモデルであるブラック・ショールズ・マートンのオプション価格モデルは、正規分布を前提とした確率微分方程式(図2)。その取扱いの簡単さから、多くの金融機関ではそれに補正を行った修正モデルが使われていました。

特に、ローンや社債を寄せ集めて作成されたCollateraized Dedt Obligations (CDO)にはガウシアンコピュラという関数を導入されていました。これは上記の正規分布(ガウス分布)を使用したもので、実際の市場で観測された値よりも、極端な変動の部分が過小評価されていました。
もし、市場が正規分布でなくファットテールを含む分布であれば、市場はランダムウォークにならないので、未来の株価予測はできるのではないかと考えられます。
2.株価の過去に対する依存性
株価が過去に依存するか(テクニカル分析が通用するか)については、いくつか調べる方法があります。
- 株価の短期記憶性→自己相関関数
- 株価の長期記憶性→R/S統計とハースト指数
自己相関関数(とは、ある時点t[n]での株価と、その前のt[n-1]での株価の相関係数になります。図のように表せます。相関係数は統計学でなじみのあるものですね。ある時間間隔τに対して自己相関関数を調べ、それが無相関になるまでの時点で、短期記憶性を持つことを判定できます。

R/S統計とハースト指数は、1951年にHarold Edwin Hurst(ハースト)という水理学者が、ナイル川ダムの貯水量をどう調整するか?という問題に対して導入しました。
R/S統計Qを計算するには
- 時系列データXとその偏差X’
- 調整域R:偏差の累積和Y=ΣX’の最大値Ymaxと最小値Yminの差
- X’の標準偏差S
がそろっていれば計算可能です。
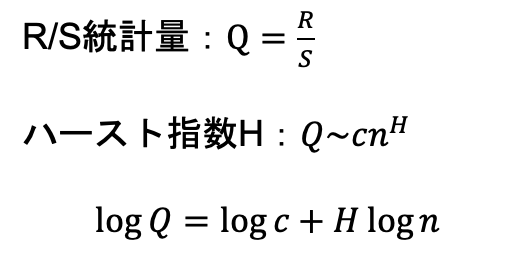
実は、ハースト指数Hが0.5である時、観察値がランダムウォークとなると判断できるのです。また、H>0.5のときランダムウォークでなく、長期記憶性を持ちます。これにより、株価の過去に対する依存性を調べられ、株価の予測可能性について調べられます。
3.まとめ
ここでは、ファットテールと株価に関する依存性を調べる方法について述べました。次回、これらについて実際の株価やインデックスに適用した例を用いて検討し、その結果を書きたいと思います。