ここでは、以前の記事で触れた株価の予測可能性について、経済学における効率的市場仮説(Efficient Market Hypothesis)の観点から説明します。記事のトップ画像は、harikichiの作成した疑似株価のシミュレーションです。
今回のキーワードは以下です。
- 効率的市場仮説
- ランダムウォーク
- ブラウン運動
1.効率的市場仮説(Efficient Market Hypothesis)とランダムウォーク
突然ですが、ランダムウォークという言葉を聞いたことがあるでしょうか?株式投資関連の本で目にした方もいると思います。専門的には難解な数学の理論を使って説明されます。
ランダムウォーク:独立同分布な確率変数の和。
これだけでは意味がわかりませんね… そこで例え話をします。
ランダムウォークとは酔歩とも呼ばれ、その名前の通り、あたかも酔っ払いの千鳥足のように予測できない動きをすることに例えられます。
図1は直近の日経平均の1年チャートですが、2〜3月に大暴落が起きましたね。1年前にこのような動きは予測できないので、ランダムウォークと呼べるのではないでしょうか。
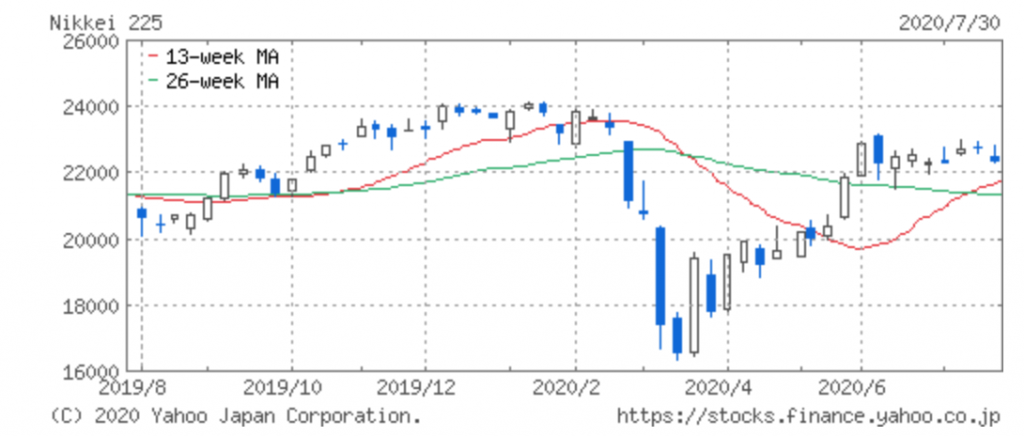
株価がランダムウォークであるなら、酔っ払いの千鳥足が予想できないように、
株価の将来の価格変化は過去の株価と無関係
ということを意味します。つまり、過去の株価から未来の株価は予測できないと言えます。そうなると、テクニカル分析は意味がないということになります。
それでは、実際に株価はランダムウォークなのでしょうか?
実は、株価がランダムウォークであることが成立するための条件の一つとして、冒頭の
効率的市場仮説
が成立していることが必要です。それは米国の学者のFamaが以下で定義しました。
利用可能なすべての情報は価格に反映されている。
(Eugene Fama, Efficient Capital Market: A Review of Theory and Empirical Work. Journal of Finance 25, 383-417.)
さらに、市場の効率性の程度には以下の三段階があります。
ウィークフォームの効率性:株価の時系列データが価格に織り込まれている。
セミストロングフォームの効率性:株価の時系列データ、企業の財務データ、株式分割の情報などを含む一般の公開データが価格に織り込まれている。
ストロングフォームの効率性:上記に加えインサイダー情報(非公開の情報)を含むすべての情報が価格に織り込まれている。
テクニカル分析を使用して収益を上げようとするならば、1.のウィークフォームの効率性が株式市場で確認されると困るわけです。なぜなら、ウィークフォームの効率性の下では、株価の時系列データはすべて織り込まれていることになり、過去の株価を読むことは意味がなくなるからです。
2. 公平な賭け、ランダムウォーク、ブラウン運動
では、実際の株式市場がどの程度効率的(あるいは効率的でない)のでしょうか?詳細な議論は避け、概要を書きます。
株式市場が効率的である時、以下が成立することがわかっています。
現在までのすべての情報を使って利益を得られない時、株価の自然対数は公平な賭け:マルチンゲールであるという。
公平な賭けというのは、参加者が全員ズルができないということです。
さらに、株価(の自然対数)がランダムウォークならば、以下のようになります。
価格変化が過去の株価とは無関係である。新しく得られた情報のみで価格は変化する。
この株価の動きを数学モデルのブラウン運動(ランダムウォークの極限)で表現した人物がいます。フランスのLouis Bachelier(ルイ・バシュリエ、図1)です。さらに、その研究を発展させて幾何ブラウン運動で表現したのが、有名なアメリカの経済学者Paul Samuelson(ポール・サミュエルソン)です。

一次元ブラウン運動で疑似的な株価チャートを作れます(図2)。実際の株価のように見えますね。
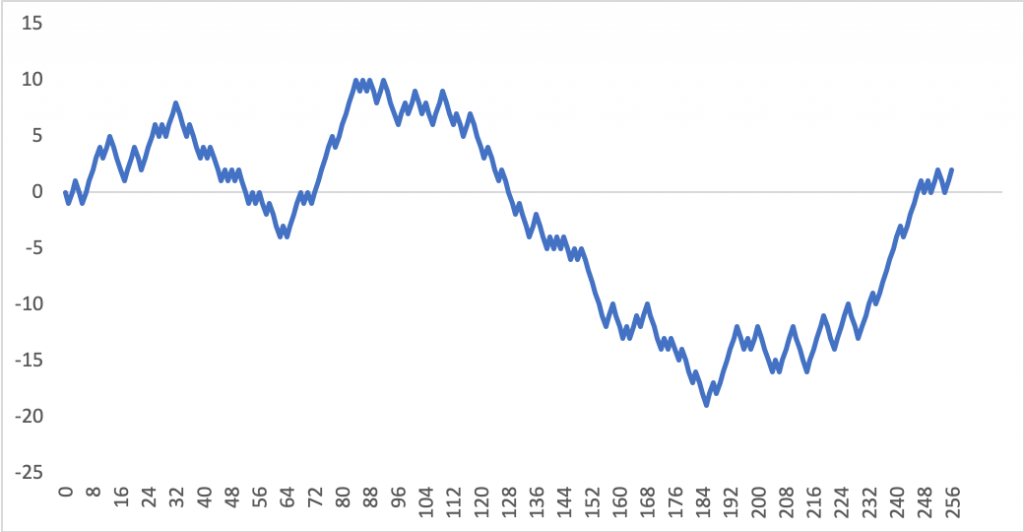
実際の株価がブラウン運動で説明できれば、以下が観察されます。
株価の対数収益率が、正規分布になる(ランダムウォークは正規分布に限らない)。
株価の時系列に相関が無い。つまり、過去のデータと将来のデータは関係ない。
この正規分布というのが曲者です。2008年のリーマンショックは複雑な金融商品(CDO)が引き金になりましたが、その基礎をなすのが正規分布を拠り所としていた金融工学になります。
次回、上記について詳しく見ていきます。

